想起来几年前，有次面试，面试官出了道算法题问： 一个数组下标0是0，1是1，2是1，3是2，4是3，求第N是多少？

当时并没有动态规划的概念，就在递归求解

var func = function(n) {
  if(n<=1) return n
  return func(n-1) + func(n-2)
};

而后面试官又问我有没有其他解，因为当时水平有限，并没有回答，后来回去查了发现这就是斐波那契数，有一种叫动态规划的算法。

动态规划 #

动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题，为了避免多次解决这些子问题，它们的结果都逐渐被计算并被储存，从简单的问题直到整个问题都被解决。因此，动态规划储存递归时的结果，因而不会在解决同样的问题时花费时间。

动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

用动态规划解决问题时，要遵循三个重要步骤：

(1) 定义子问题；
(2) 实现要反复执行来解决子问题的部分；
(3) 识别并求解出边界条件。

动态规划解

var fib = function(n) {
  const dp = [0,1]
  for(let i=2;i<=n;i++){
    dp[i] = dp[i-1]+dp[i-2]
  }
  return dp[n]
} 

但是会对为什么是dp[i-1]+dp[i-2]感到很疑惑，所以以另一道题爬楼梯来演示一遍

爬楼梯 #

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

题意 #

如果了解动态规划，和做过上面的斐波那契数，就能联想到这其实就是一种斐波那契数的变体，然后就会直接写出dp[n] = dp[n-1] + dp[n-2]，那到底为什么是n-1+n-2呢？

为何是(n-1) + (n-2) #

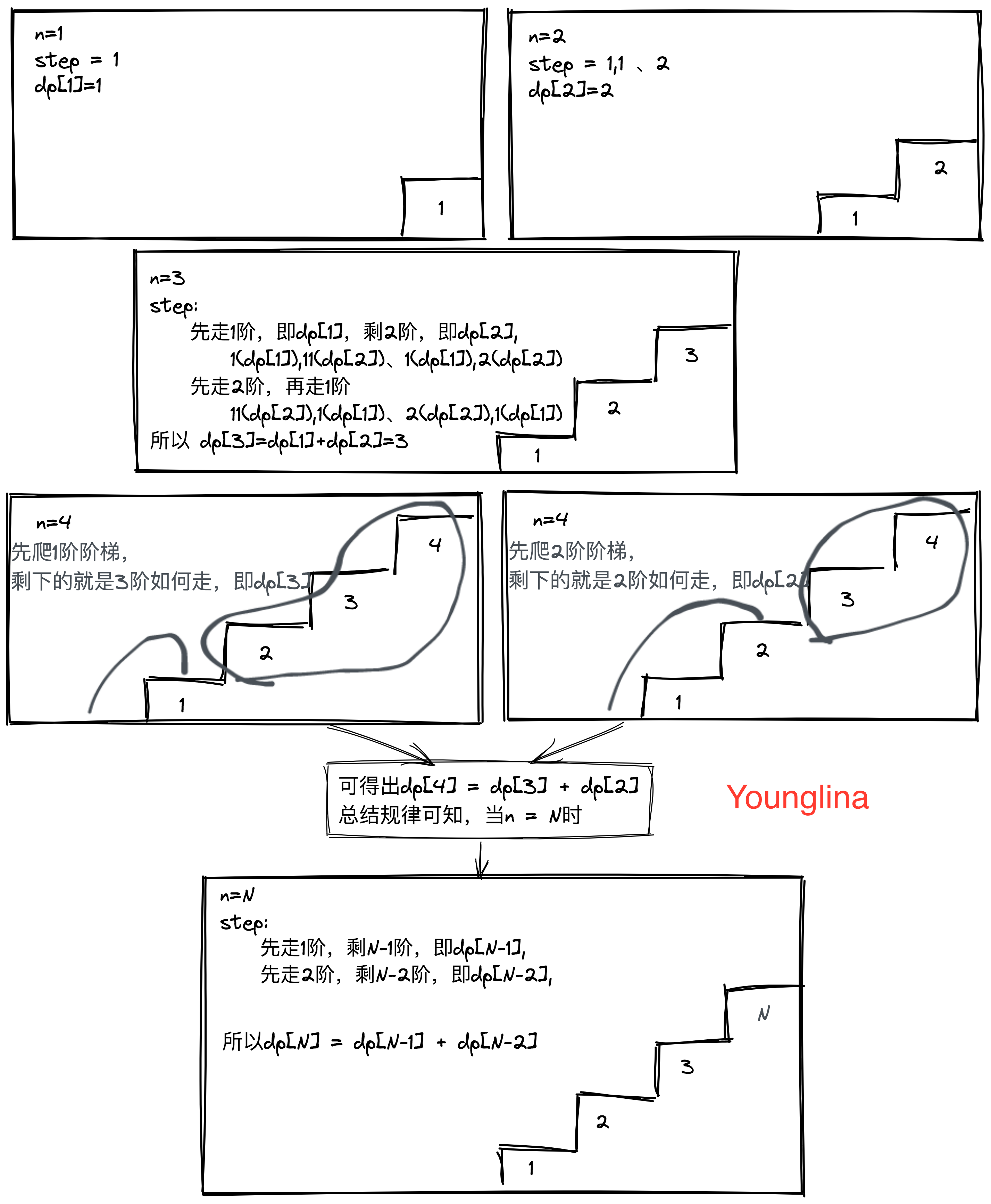
题解 #

动态规划

var climbStairs = function(n) {
    const dp = [1,1] 
    for(let i=2;i<=n;i++){ 
        dp[i] = dp[i-1]+dp[i-2] 
    } 
    return dp[n] 
};

优化
因为要的只是最后一个值，可以使用滚动数组，优化空间

var climbStairs = function(n) { 
    if(n<=2) return n 
    const dp = [1, 2]
    for(let i=3;i<=n;i++){ 
        let sum = dp[1] + dp[2] 
        dp[1] = dp[2] 
        dp[2] = sum 
    } 
    return arr[2] 
};

之前没有弄懂为什么是dp[n-1]+dp[n-2]时，觉得就是应该这样，就背下来，现在弄懂了之后，觉得顺其自然，不用强行去背了，联想一下就能知道是为什么。