题目描述 #

11. 盛最多水的容器
给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

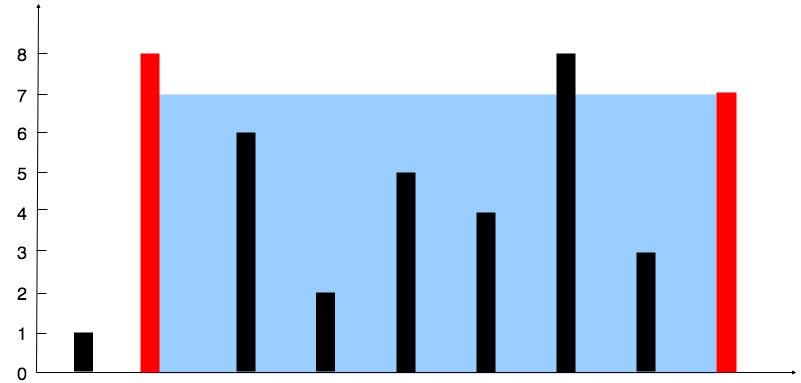
示例 1： #

输入：[1,8,6,2,5,4,8,3,7]  
输出：49  
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2： #

输入：height = [1,1]
输出：1

示例 3： #

输入：height = [4,3,2,1,4]
输出：16

示例 4： #

输入：height = [1,2,1]
输出：2

思路 #

参考宫水三叶
先用两个指针 i 和 j 指向左右边界，然后考虑指针应该怎么移动。

由于构成矩形的面积，取决于 i 和 j 之间的距离（记为 w） 和 i 和 j 下标对应的高度的最小值（记为 h）。

首先无论是 i 指针往右移动还是 j 指针往左移动都会导致 w 变小，所以想要能够枚举到更大的面积，我们应该让 h 在指针移动后变大。

不妨假设当前情况是 height[i] < heigth[j]（此时矩形的高度为 height[i]），然后分情况讨论：

• 让 i 和 j 两者高度小的指针移动，即 i 往右移动：

  • 移动后，i 指针对应的高度变小，即 height[i] > height[i + 1]：w 和 h 都变小了，面积一定变小
  • 移动后，i 指针对应的高度不变，即 height[i] = height[i + 1]：w 变小，h 不变，面积一定变小
  • 移动后，i 指针对应的高度变大，即 height[i] < height[i + 1]：w 变小，h 变大，面积可能会变大

• 让 i 和 j 两者高度大的指针移动，即 j 往左移动：

  • 移动后，j 指针对应的高度变小，即 height[j] > height[j - 1]：w 变小，h 可能不变或者变小（当 height[j - 1] >= height[i] 时，h 不变；当 height[j - 1] < height[i] 时，h 变小），面积一定变小
  • 移动后，j 指针对应的高度不变，即 height[j] = height[j - 1]：w 变小，h 不变，面积一定变小
  • 移动后，j 指针对应的高度变大，即 height[j] < height[j - 1]：w 变小，h 不变，面积一定变小

综上所述，我们只有将高度小的指针往内移动，才会枚举到更大的面积：

题解 #

var maxArea = function(height) {
  let i=0,j=height.length-1,res=0
  while(i<j){
    res = Math.max(res, Math.min(height[i],height[j])*(j-i))
    height[j]<height[i] ? j-- : i++
  }
  return res
};