Appearance
题目描述
96.不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
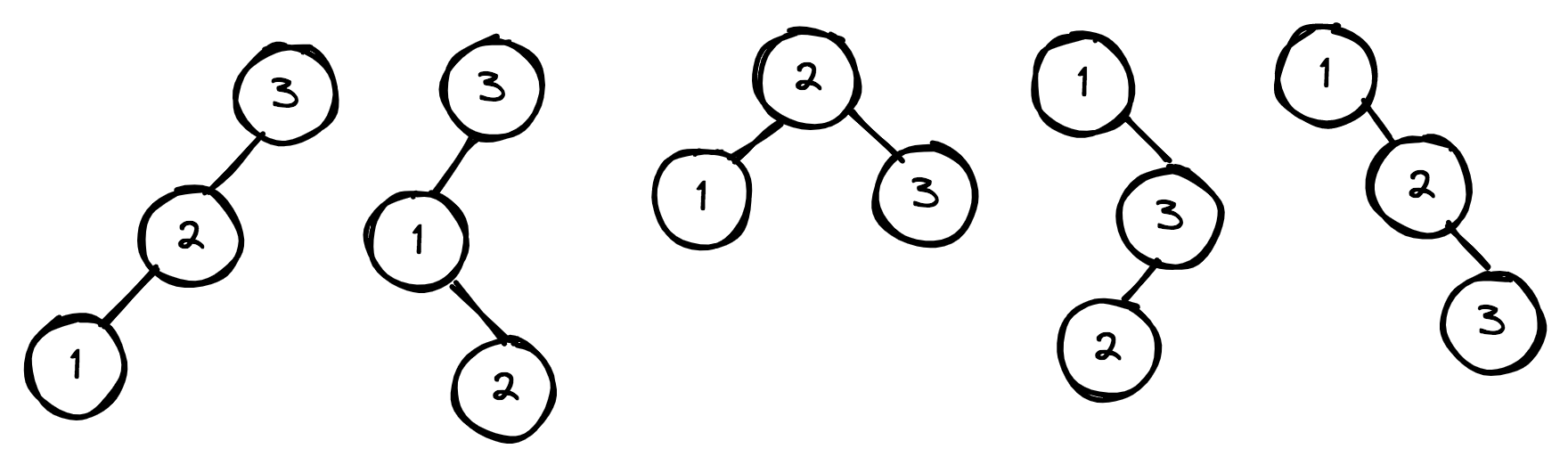
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示
1 <= n <= 19
思路1 动态规划
题意是搜索二叉树的种数,搜索二叉树是,左节点小于根节点,右节点大于根节点。
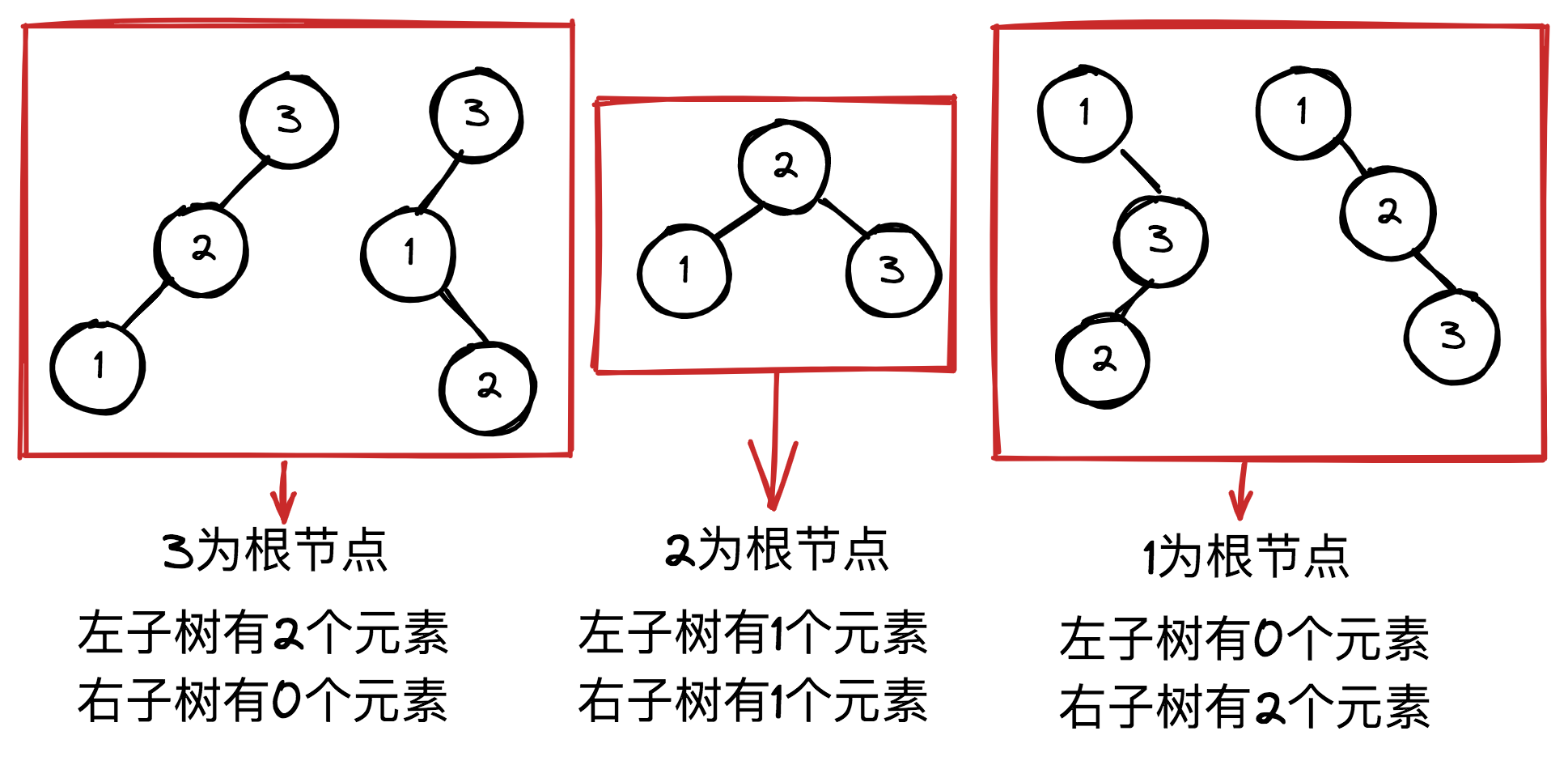
通过实例1可以看出,当n=3时,分别以3,2,1为根节点的情况3为根节点搜索树的数量 = 左子树有2个元素的情况 * 右子树有0个元素的情况2为根节点搜索树的数量 = 左子树有1个元素的情况 * 右子树有1个元素的情况1为根节点搜索树的数量 = 左子树有0个元素的情况 * 右子树有2个元素的情况
所以dp[3]=dp[2]*dp[0]+dp[1]*dp[1]+dp[0]*dp[2]
所以当有n个数字时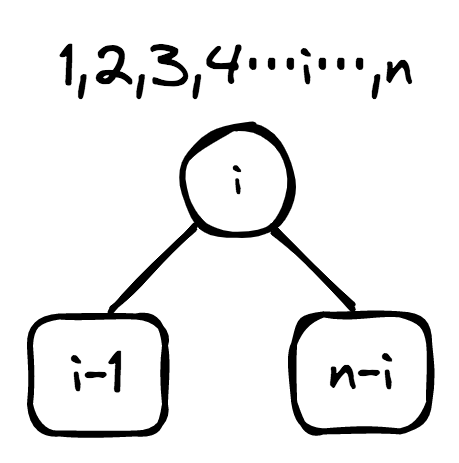
dp[n]有1到n个根节点中,有以i-1为左子树节点数量 * n-i为右子树节点数量的累加和,即dp[n] += dp[i-1]*dp[n-i]
空节点其实也算是一颗二叉搜索树,所以可以把dp[0]设置为1
题解1
javascript
var integerBreak = function(n) {
let dp = Array(n+1).fill(0)
dp[0]=1
for(let i=1;i<=n;i++){
for(let j=1;j<=i;j++){
dp[i] += dp[j-1]*dp[i-j]
}
}
return dp[n]
}
优化
其实观察可以发现,左右两边其实是对称的,dp[2]*dp[0]和dp[0]*dp[2],所以我们内部循环只要循环mid=Math.floor(i/2)次,累加和*2即可, 最后判断i是奇数还是偶数,如果是奇数,则再加上dp[i-(mid+1)]*dp[i-(mid+1]
javascript
var numTrees = function(n) {
let dp = Array(n+1).fill(0)
dp[0] = 1
for(let i=1;i<=n;i++){
let mid = Math.floor(i/2)
for(let j=1;j<=mid;j++){
dp[i] += 2* dp[j-1]*dp[i-j]
}
if(i%2!=0){
dp[i] += dp[i-(mid+1)] * dp[i-(mid+1)]
}
}
return dp[n]
}
思路2 递归
由之前的思路可知,就是根据有1到i为根节点,左边有i-1个节点,右边有n-i个节点,而i-1和n-i又各自为根节点,所以递归求和即可, 递归过程中会有很多重复计算,所以需要一个对象存储已经计算过的结果,避免重复计算
题解2
javascript
var numTrees = function(n){
let dp=[],path={}
let dfs = (n) => {
if(n<=1) return 1
if(path[n]) return path[n]
let res = 0
for(let i=1;i<=n;i++){
res += dfs(i-1)*dfs(n-i)
}
path[n] = res
return res
}
return dfs(n)
}